Mathilde vend des boules en bois, qu’elle peint à la main pour servir d’objets d’ornement. Elle souhaite pouvoir envoyer ses réalisations par la poste à ses clients. Pour cela, elle a fait confectionner des boîtes cylindriques, chacune contenant très exactement une boule. Mais Mathilde est perfectionniste : elle voudrait aussi décorer à la main la face latérale extérieure de chacun des cylindres (sans toucher au couvercle ni au fond de la boîte qui sont en métal doré du plus bel effet…).
Sachant qu’il lui faut 5 cl de peinture pour décorer une boule, combien lui faudra-t-il de peinture pour embellir chaque cylindre ?
L'énigme visuelle 16
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 15
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 1
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 3
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 22
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?
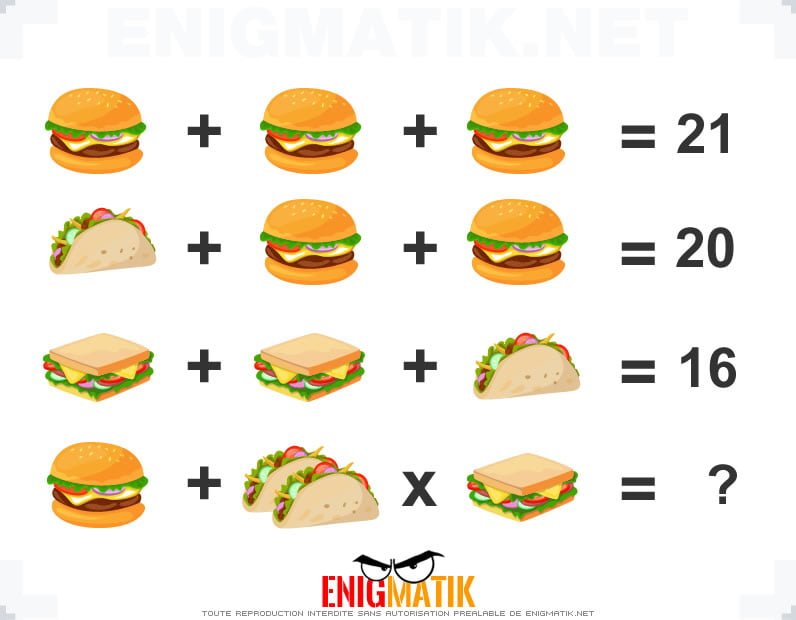
L'énigme visuelle 29
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 2
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 20
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 13
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 26
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 25
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 1
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 3
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 30
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 27
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 17
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 9
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 7
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 11
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 21
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 8
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 28
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 23
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 14
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 10
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 19
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?
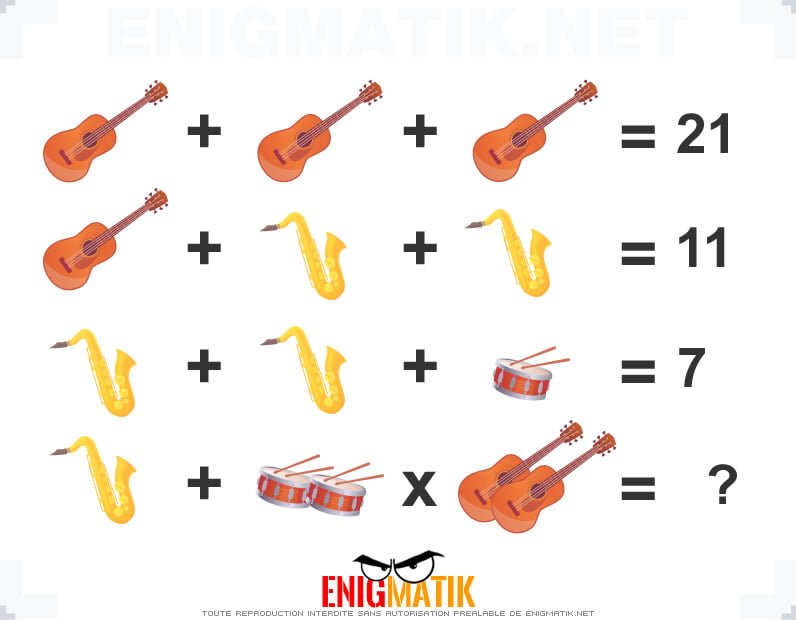
L'énigme visuelle 18
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 5
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 4
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 24
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

