Monsieur X possède 10 sacs contenant 10 pièces de monnaie dont l’aspect est identique. Un des sacs contient des fausses pièces qui pèsent 10 grammes de plus que les vraies. En utilisant une balance qui pèse en grammes, comment Monsieur X peut-il savoir quel sac contient les fausses pièces en une seule pesée ?
L'énigme visuelle 27
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 2
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 29
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 26
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 22
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?
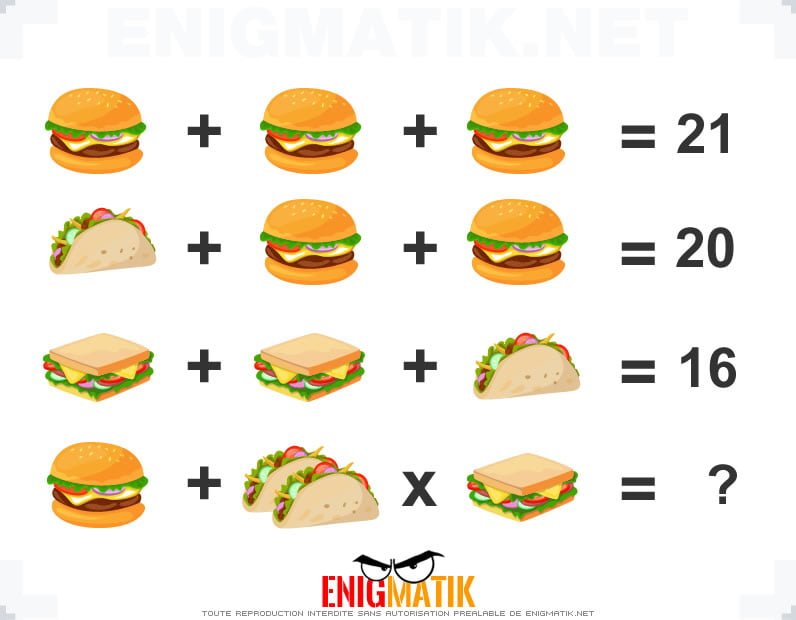
L'énigme visuelle 19
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?
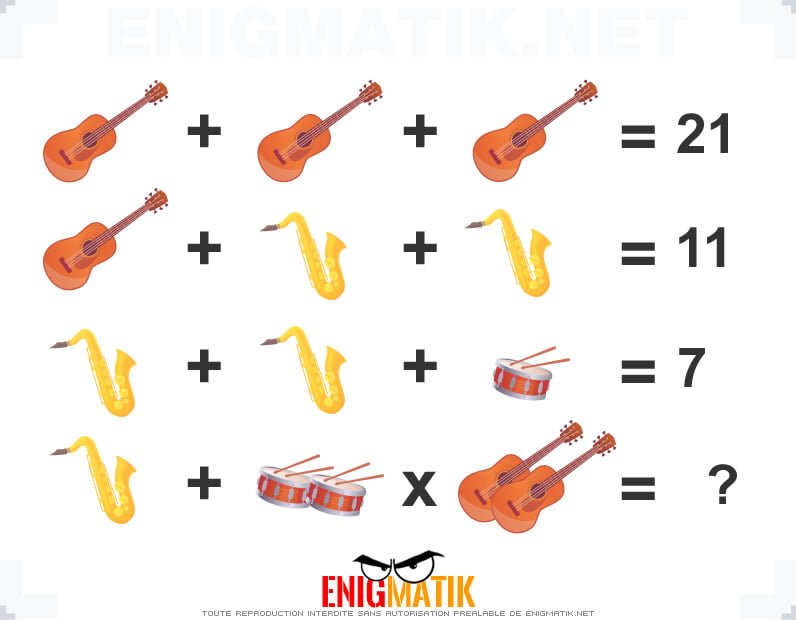
L'énigme visuelle 11
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 7
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 20
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 24
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 28
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 10
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 18
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 3
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 13
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 25
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 21
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 16
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 1
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 17
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 5
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 1
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 14
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 23
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 3
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 9
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 4
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 15
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 30
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 8
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

