La maison d’Annie est située tout au sommet d’une colline. Pour aller au village qui se trouve à 3,240 km d’ici, au pied de ce monticule, elle met d’habitude six minutes de moins que pour revenir et remonter la côte jusque chez elle. En fait, elle a constaté qu’elle allait deux fois et demi plus vite dans le sens de la descente que dans le sens de la montée…
Mais combien de temps lui faut-il d’habitude pour descendre au village ?
L'énigme visuelle 5
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 28
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 17
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 8
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 21
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 24
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 25
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 1
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 30
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 3
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 27
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 9
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 10
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 1
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 3
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 23
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 19
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?
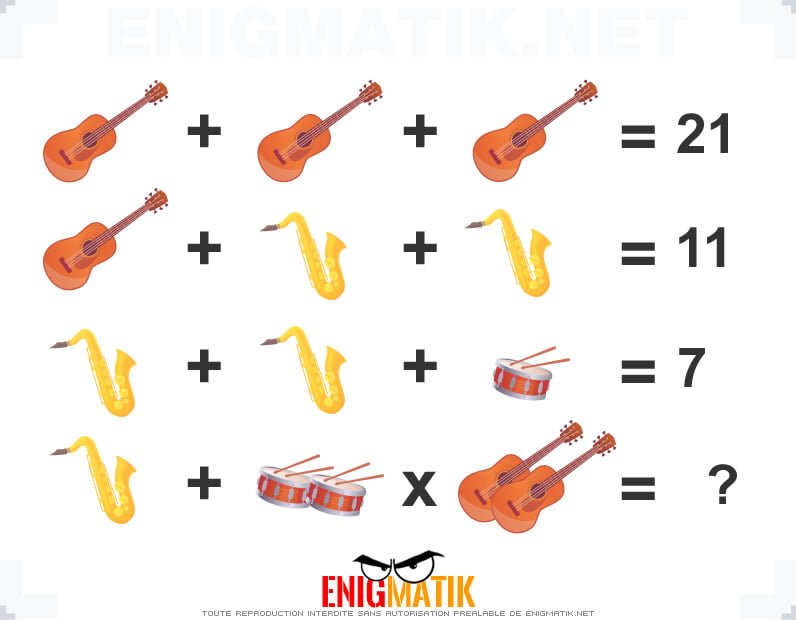
L'énigme visuelle 16
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 18
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 20
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 22
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?
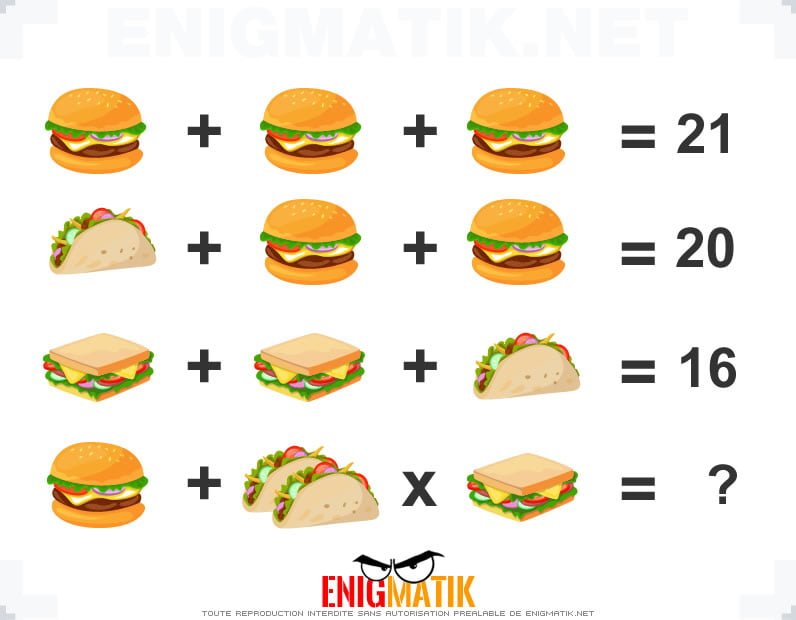
L'énigme visuelle 29
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 13
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 2
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 26
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 11
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 15
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 4
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 14
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 7
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

