Il avait beaucoup plu, sur cette planète, pendant fort longtemps.
Sur la place centrale d’un village abandonné trônait un pluviomètre, capable de contenir au maximum un demi-litre. Sur ce pluviomètre, des dessins racontaient l’histoire suivante :
Au soir du jour ou ce pluviomètre fut installé, il contenait déjà 1/3 de litre. Mais à partir de ce jour précis, la pluie a commencé à diminuer. Les anciens habitants de cette planète ont constaté qu’il tombait chaque jour trois fois moins d’eau que la veille. Ainsi, par exemple, il tomba le deuxième jour 1/9 de litre, le troisième jour 1/27 de litre… Finalement, il n’y eut plus assez d’eau pour abreuver les habitants, qui finirent par disparaître quelques centaines d’années plus tôt…
En supposant que l’humidité de l’air soit suffisante pour avoir empêché l’évaporation de l’eau du pluviomètre, en supposant aussi que personne n’ait touché à son contenu, en supposant enfin qu’il ait continué à pleuvoir chaque jour trois fois moins que la veille, le pluviomètre était-il plein le jour où il fût découvert ?
L'énigme visuelle 15
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 18
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 5
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 17
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 30
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 24
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 1
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 25
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 16
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 14
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 26
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 1
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 27
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 3
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 22
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?
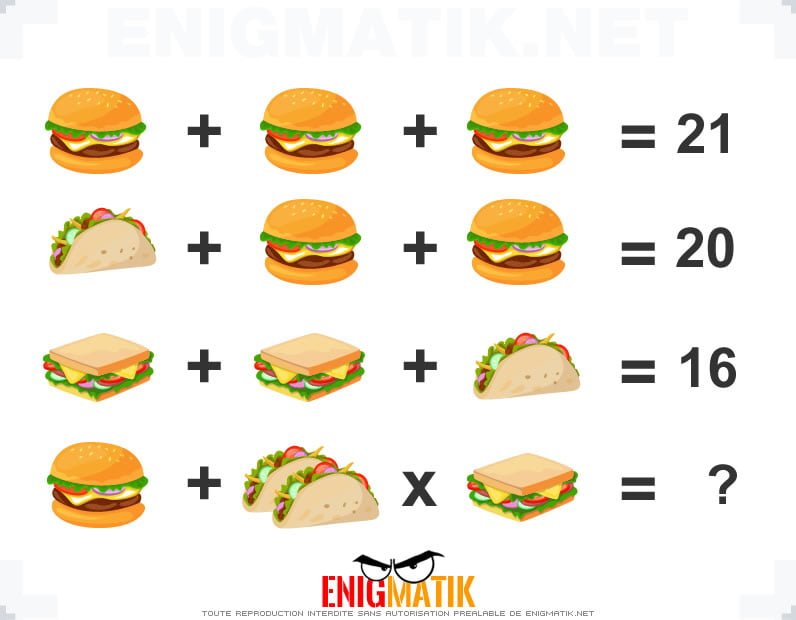
L'énigme visuelle 10
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 21
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 2
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 23
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 28
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 20
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 19
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?
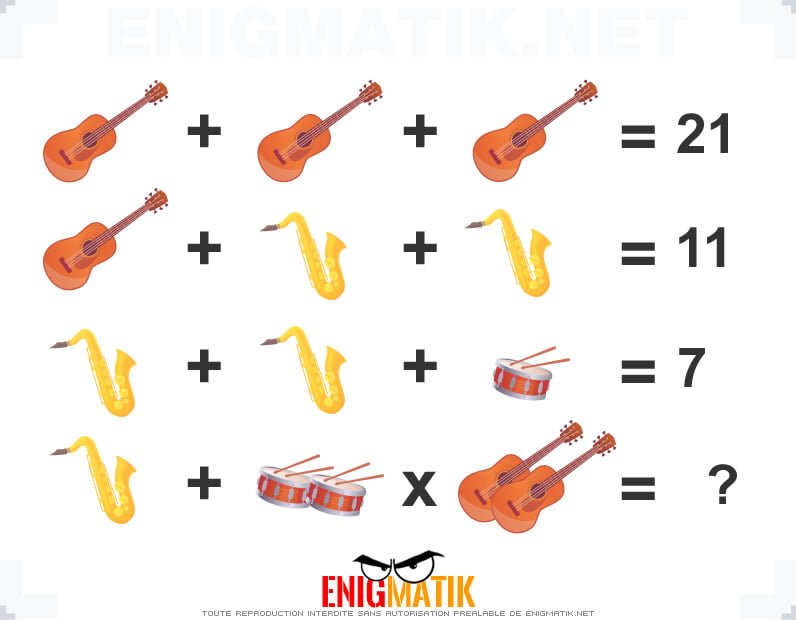
L'énigme visuelle 13
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 7
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 3
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 11
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 8
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 29
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 9
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 4
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

