L’énigme se passe dans un monastère très strict où vivent 40 moines. Ces moines ont pour seule vocation la prière et ils ne doivent absolument pas communiquer entre eux, ni par geste, encore moins par la parole.
Ils ne peuvent même pas se regarder dans un miroir. Chaque jour, le père supérieur, seul à pouvoir parler, réunis les moines en salle de réunion pour les informer des nouvelles du jour.
Une maladie très dangereuse et peut être contagieuse vient d’arriver chez les moines. Elle se caractérise par la présence de petites plaques rouges sur le visage, bien visibles mais non douloureuses. Elle ne provoque pas d’autres symptômes au début. Chaque moine ne peut donc pas savoir s’il est malade.
Le père supérieur décide de prévenir les moines. Lors de la réunion quotidienne, il les informe que cette maladie est dangereuse. Le père supérieur demande qu’à la fin de chaque réunion, tous ceux qui se savent malades, préparent leurs valises et partent du monastère.
A la fin de cette réunion, le père supérieur demande : « Que tous ceux qui se savent malades se lèvent et s’en aillent ». Mais personne ne se lève.
Le lendemain, à la fin de la réunion, le père supérieur demande : « Que tous ceux qui se savent malades se lèvent et s’en aillent ». Mais personne ne se lève.
Le surlendemain, à la fin de la réunion, le père supérieur demande : « Que tous ceux qui se savent malades se lèvent et s’en aillent ».
A ce moment-là, tous les moines qui sont malades se lèvent et s’en vont.
Combien sont-ils ?
L'énigme visuelle 10
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 3
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 27
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 4
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 14
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 28
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 11
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 25
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 29
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 13
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 21
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 1
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 2
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 23
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 30
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 9
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 26
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 16
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 19
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?
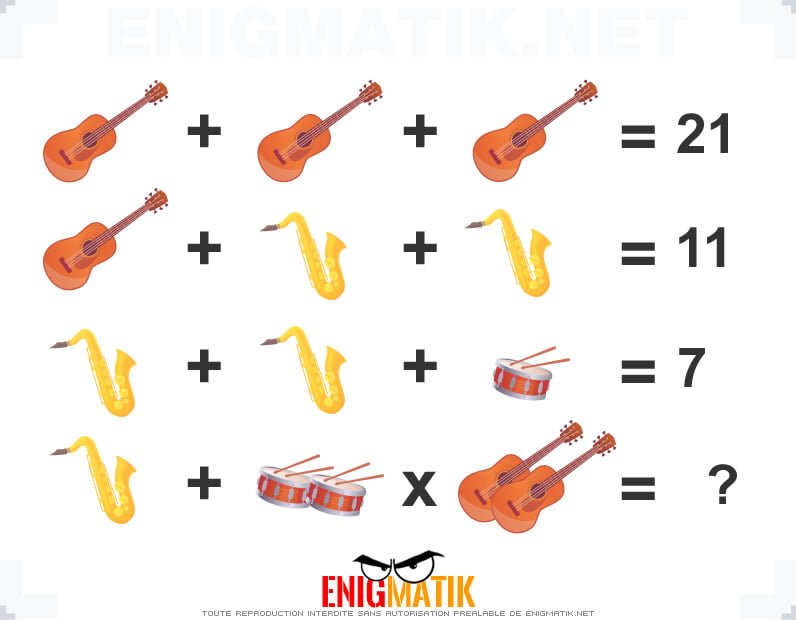
L'énigme visuelle 1
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 3
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 7
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 22
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?
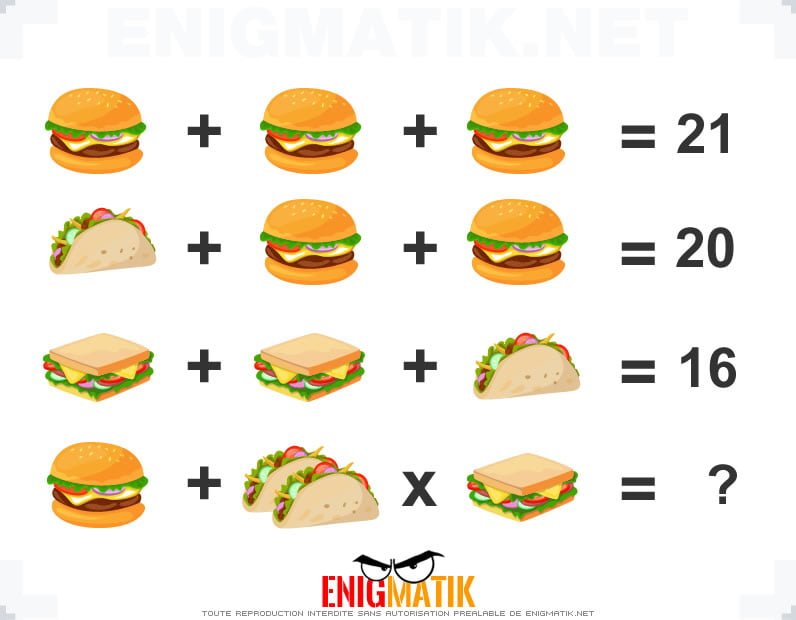
L'énigme visuelle 17
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 24
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 20
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 15
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 5
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 18
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

L'énigme visuelle 8
Nous vous proposons un casse-tête "image". Saurez-vous trouver la solution à cette énigme sans tricher ?

